FLATLAND PROJECT
THE CULTURAL EXPERIENCE BY KARTHIK SADANAND
Polygons in Flatland are like humans in Spaceland. (Spaceland is the land of three dimensions.) Polygons are also very different than human beings. We can distinguish different people fairly easily, but this is not the case for the polygons. When a polygon sees another polygon (or for that matter, any figure), they can only perceive that figure as a straight line. They are not gifted with the birds-eye view that we have in Spaceland, for they have no concept of height. Here is an example:
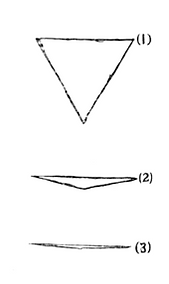
Drawing (1) illustrates the view that we in Spaceland have of an equilateral triangle. We are able to see all three sides and all three angles.
Drawing (2) illustrates our view becoming closer and closer to that of a Flatlander.
Drawing (3) illustrates an almost picture perfect view of a Flatlander. Eventually, we would level with the triangle and see a straight line.
The following problem arises: If these polygons can only see each other as straight lines, then how do they distinguish among themselves?
There are three ways that the Polygons can do this. They are as follows:
(1) Hearing
(2) Feeling
(3) Sight
The first way polygons can distinguish among themselves is by the method of hearing. Polygons have a highly developed sense of hearing and are able to use this to discriminate between social classes. (The social class system of Flatland is a true mess which I will explain later.) This method is flawed, however. Hearing can only be used to distinguish between the three lowest classes: Equilateral Triangle, Square, and Pentagon. As the number of sides go up, it is harder to tell apart from the different voices of the polygons. Some Isosceles triangles also possess the ability to change their voice to that of a Circle's. Therefore, this method is not commonly used.
The second way polygons can distinguish among themselves is by the method of feeling. Feeling is the most commonly used method of recognition in Flatland for the lower classes. Feeling does not mean that one polygon must completely move around the perimeter of another to identify it. Polygons are trained in school to be able to identify the angles of an Equilateral Triangle, Square, and a Pentagon from the slightest touch. It becomes difficult again once we are dealing with polygons of more sides than a Pentagon. This brings us to the last method of recognition.
The third way polygons can distinguish among themselves is by the method of sight. This may seem a bit hypocritical, as I stated above that all polygons register other figures as straight lines. Polygons can use their sense of sight to identify different polygons with the help of a natural phenomenon of Flatland - the Fog. The Fog causes the straight lines perceived by the polygons to appear at varying levels of dimness.
Here is an example:
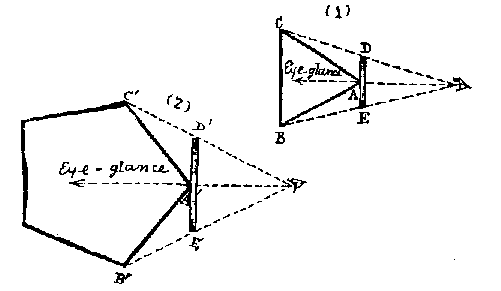
These are two illustrations of the views a polygon may have of a Equilateral Triangle and a Pentagon.
When the eye is placed so that the angle A is bisected, sides CA and AB will appear to be congruent.
With the Equilateral Triangle in Drawing (1), a polygon will see the straight line DE. The bisector of line DE is seen as point A. Point A will appear very bright as it is closest to the polygon. The two ends of the line will appear to fade away into the Fog rapidly because the sides recede relatively rapidly. (This is due to the 60 degree interior angle of an Equilateral Triangle.)
It is a bit different with the Pentagon in Drawing (2). We will again perceive a straight line D'E. The bisector A' will appear bright just as last time, but the two extremities of the line will fade away less rapidly. This is because of the 108 degree interior angle of a Pentagon.
It is seen here that the larger a Polygon's angle is, the brighter the extremities of the line are. This method is used by the more educated residents of Flatland who consider themselves to be too high and mighty to resort to Feeling. Speaking of the more educated residents of Flatland, let's move on to the concept of social classes in Flatland.